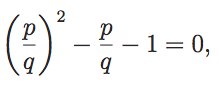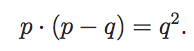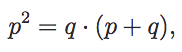Mal mathematisch...
Der Goldene Schnitt ist dasjenige Teilverhältnis, bei dem sich die Länge der ganzen Strecke zur längeren so verhält wie die längere zur kürzeren. Nennen wir die längere Seite a und die kürzere b, so erhalten wir

Da die Strecke a nur eine positive Länge haben kann, kommt nur die erste Lösung in Frage. Der Goldene Schnitt ist also (1 + √5)/2. Er ist damit Lösung der Gleichung x2 − x − 1 = 0. Der Goldene Schnitt ist irrational. Es war für die alten Griechen ein großer Schock, als sie dies erkannten, da sie der festen Überzeugung waren, jede Zahl sei als Bruch darstellbar. Die Irrationalität lässt sich allein anhand der Definition beweisen: Wäre der Goldene Schnitt rational, so müssten p, q existieren, so dass gilt
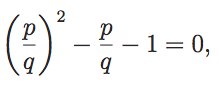
wobei der Bruch p/q so weit wie möglich gekürzt sein soll. Daraus folgt
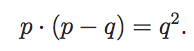
Diese Gleichung besagt, dass p die Zahl q2 teilt. Da p und q teilerfremd sein sollten, muss p = 1 sein. Addiert man stattdessen p x q zu obiger Gleichung, so erhält man
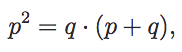
was heißt, dass q die Zahl p teilt, also ist auch q = 1. Aber p = q = 1 ist keine Lösung für die quadratische Gleichung am Anfang, was zu einem Widerspruch führt. Also ist der Goldene Schnitt irrational!
Etwas anders verhält es sich mit Fibonacci:
Nach der Rekursionsgleichung lässt sich der Quotient sukzessiver Fibonacci-Zahlen wie folgt berechnen:

Das ist aber nicht anderes als ein
Näherungswert für den Goldenen Schnitt. Daraus folgt, dass der Quotient sukzessiver Fibonacci-Zahlen für n → ∞ gegen den Goldenen Schnitt konvergiert!
LG
Wilhelm